From the microscale to the mesoscale

Similarity at the mesoscale

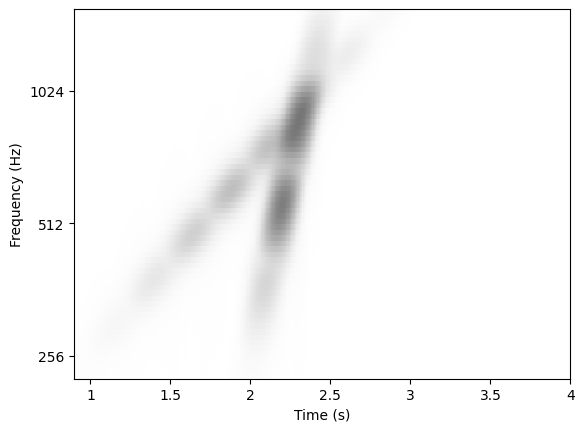
Two AM chirps, \(x\) and \(x'\), are illustrated above in the time-(log)frequency domain. They are displaced in time from on another by \(2^{11}\) samples at a sampling rate of \(2^{13}\) Hz. They differ in chirp rate by a factor of 4. Clearly we can see that when the events are unaligned, distance computation becomes unreliable at the microscale, i.e. between short-time spectra. Time–frequency representations such as the Mel spectrogram, MFCCs, or the CQT are adequate representations of similarity upto the scale of 10ms (i.e., the typical frame size) and when two signals are aligned in time. If the two chirps had equal chirp rate, they would be maximally disjoint, hence the norm could become as large as \(2|x|\). Despite displacements in time, our perception of how acoustically similar they sound remains. Hence we need a distance representation that reflects similarity in mesostructure, that is, time-frequency evolution beyond the microscale.

The moving image above illustrates the need for a similarity representation that goes beyond short-time Fourier analysis. The black and grey bars illustrate the distance between the two chirps in JTFS space and multiscale spectrogram space. We can see that the JTFS loss is at a minimum when the two chirps are of equal chirp rate, while the distance increases as the chirp rate moves increasingly further from the target. This is not the case for the MSS distance: the distance is not correlated with the discrepancy in chirp rate. In fact, the distance begins to increase when the chirp rates are equal, illustrating the inefficacy of the MSS distance for measuring similarity in spectrotemporal modulations.

Invariance to time-shifts

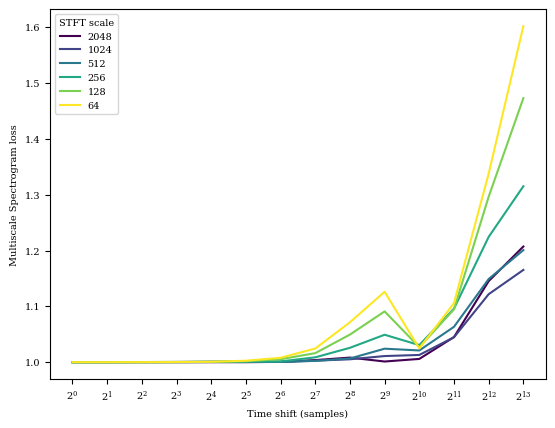
Note that \(S_1\) is only invariant to time-shifts upto a support of \(T\).